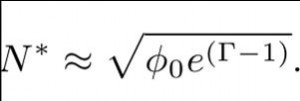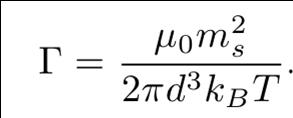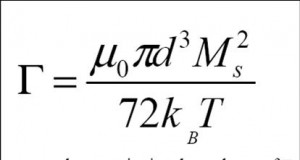Will my magnetic particles separate so fast?
Commercial magnetic beads separate in seconds when you approach a magnet. The micrometer size and an appropriate magnetic charge do the job. However, when the size and/or the magnetic content decreases, separation time can increase to many hours.
I have been travelling around the globe on scientific meetings, sales call, workshop and seminars related with magnetic beads. There I was showing the performance of precision magnetophoresis systems my company was producing (www.sepmag.eu). After the demo, the people working on new applications of magnetic beads and/or producing nanobeads always asked me ‘Will my magnetic particles separate so fast?’
The answer is not easy. Fortunately my former colleagues at Universitat Autonoma de Barcelona campus are working hard on finding the answer (honestly, the discussion started at a lunch initially planned to talk about family, films and football).
We first we focused on understanding how the magnetic beads are separated: in short, when a big magnetic field is applied, the magnetic beads become saturated and, as any small magnet, align with the neighbour beads. This large chains gains magnetic moment as a whole and move faster than an isolated magnetic bead will do. If the beads are superparamagnetic, once the magnetic field disappears, the chains dissolved and the beads disaggregate by simple thermal diffusion.
The answer to a question opened a lot of new ones: Which parameters determine the chain-like aggregate formations? Or in simple words, when my beads will move fast (seconds) or slow (hours).
The short answer is that it will depend mainly on the magnetic moment of each single bead and their diameter, and slightly on the beads concentration.
With these three parameters, we can estimate the number of magnetic beads in the chains: if N>>1 your beads will separate quickly. If N<1 your beads will separate as isolated particles, then separation time will be large. I’ll not come on details on the simulations and calculations, if you are interested you can have a look on the published papers. But we can have a look on the resulting formula:
Number of magnetic beads on a chain when a magnetic field is applied
The number of beads will depend on the volume fraction, of dispersed solids in the suspension (easily calculated from concentration). Increasing the concentration a factor 4, the N* will double. But if your beads are slow (N<<1), it will be difficult in practice to change the concentration by several orders of magnitude.
The second part of the expression, is the gamma factor. As N depends exponentially on it, any small change will affect a lot to the N.
But what is gamma? My colleagues described as
Factors affecting exponentially the number of magnetic beads on chains, original formula
Apart of physical constants m0 and kB, we have temperature, something we can’t vary too much in Life Sciences, the saturation magnetic moment of the bead and their diameter. Note we are assuming the bead is saturated, i.e. the magnetic field applied is big enough (we have did the calculations for not-saturated case, but has less practical use for biomagnetic separation as the process time are much more longer…)
As experimental physicist, I prefer to express gamma as function of saturation magnetisation, Ms the value we can measure experimentally (Note Ms with capital ‘M’, is the magnetisation by unit of volume. If you measure magnetisation by unit of mass –emu/g-, just multiply by the beads density)
Factors affecting exponentially the number of magnetic beads on a chain, as I prefer to express
With this expression you can see the quantitative dependence of gamma: it growths as the cube of the bead diameter and the square of Ms.
How to take advantage of the theory to increase the performance of your beads?
We can calculate our N* using the above expressions. If the value is below 1, we can estimate the increase on diameter need to reach N>>1.
As probably, the resultant diameter will exceed the needs of your application, we should play with the magnetic properties. Increase a 10% the content of magnetic pigment will increase N* by a factor 3 (remember N is proportional to exp(d3Ms2)). It is worth a try!!
Of course, if you can change your magnetic charge by one with higher magnetisation saturation it will be better, but most probably it will affect the chemistry necessary for your beads.
I hope to have been able to help you to use the work of my colleagues for practical applications. If you wish go through the details, have a look on the references or send me an e-mail (martinez@sepmag.eu) if you need help to determine your N*.
References:
J. Andreu, J. Camacho, J. Faraudo. Aggregation of superparamagnetic colloids in magnetic fields: the quest for the equilibrium state. Soft Matter 7, 2336 (2011).
J. Andreu, J. Camacho, J. Faraudo, M. Benelmekki, C. Rebollo, Ll.M. Martinez. Simple analytical model for the magnetophoretic separation of superparamagnetic dispersions in a uniform magnetic field. Phys. Rev. E 84, 021402 (2011).